What are component and system reliability and how it can be improved?
Module III Product Quality Improvement
Lecture – 2 What are component and system reliability and how it can be improved?
Reliability is a measure of the quality of the product over the long run. The concept of reliability is an extended time period over which the expected operation of the product is considered and we expect the product will function according to certain expectations over a stipulated period of time. With the customer and warranty costs in mind, we must know the chances of successful operation of the product for at least a certain stipulated period of time. Such information helps the manufacturer to select the parameters of a warranty policy.
Technically, reliability is the probability of a product performing its intended function for a stated period of time under certain specified conditions. Four aspects of reliability are apparent from this definition first, reliability is a probability of success-related concept; the numerical value of this probability is always between 0 and 1. Second, the functional performance of the product had to be measured under certain stipulated conditions. Product design is expected to ensure development of a product that meets or exceeds the specified requirements under specified operating conditions. For example, if the breaking strength of a nylon cord is expected to be 1000 kg, then in the predefined operational conditions, the cord must be able to bear weights of 1000 kg or more. Third, reliability implies successful operation over a certain period of time (t). Although no product is expected to last forever, the time dimension ensures satisfactory performance over at least a minimal stated period (say, 100 hours). In the context of these three aspects, the reliability of the nylon cord might be described as having a probability of successful performance of 0.92 in bearing loads of 1000 kg for 1 year under dry conditions.
It is observed that most manufacturing products go through three distinct phases (see Figure 3- 8) from product inception to wear-out.
Figure 3-8 Bathtub Curve
The life-cycle curve of Figure 3-8 shows the variation in the failure rate as a function of time in different phases. Conventionally the failure rate ( ë ) is plotted as a function of time. This curve is often referred to as the bathtub curve; it consists of the debugging (infant- mortality) phase, the chance-failure phase (useful life phase), and the wear-out phase.
The debugging phase, also known as the infant-mortality phase, exhibits a drop in the failure rate as initial problems identified during prototype testing are removed. The chance-failure phase, between times t1 and t2, is then encountered; failures occur randomly and independently. This phase, in which the failure rate is constant, typically represents the useful life of the product delivered to end customer. In the wear-out phase, an increase in the failure rate is expected due to wear and tear of the product. Here, after the end of their useful life, parts age and wear out.
For the random chance-failure phase, which represents the useful life of the product or component, the failure rate is assumed to be constant. As a result, the exponential distribution is selected to describe the time-to-failure of the product for this phase.
An exponential distribution as a memory less property and its probability density function is given by
Here, F(t) represents the cumulative distribution function at any time t. Reliability decreases exponentially with time (Figure 3-9) and the failure-rate function, say r(t) , is given by the ratio of the time-to-failure probability density function to the reliability function. We have
Figure 3-9 Reliability v/s Time
Thus, assuming an exponential distribution, r (t) implying a constant failure rate, as shown below.
Let us consider a resistor component, which follows an exponential time-to-failure distribution with a failure rate of 8% per 1000 hr. We are interested to calculate the reliability of the resister at 5000 hr, and also we intend to calculate the mean-time-to-failure. Here the constant failure rate ë is obtained as
Thus there is about 67% chance of survival (success) of the resister under stipulated conditions and stipulated time (5000 hr). The mean (average) time-to-failure (assuming it cannot be repair) of the resister will be
System Reliability
Let us consider a system with three components (say three resister) in series as shown in Figure 3-10.
Figure 3-10 Series System
Without loss of generality, if the system components can be assumed to have a time-to-failure distribution as exponential with each component has a constant failure rate, we can easily compute the reliability of n-system in series. Suppose the system has n components and in series, each with exponentially distributed time-to-failure with failure rates ë1 , ë2 ,K , ën . The system reliability is calculated as the product of the component reliabilities:
This implies that the time-to-failure of the system is exponentially distributed with an equivalent failure rate of given by
Systems with Components in Parallel
System reliability can be improved by placing redundant components in parallel. The system operates as long as at least one of the components operates. A three component parallel system is represented as given in Figure 3-11.
Figure 3-11 A Parallel Component System
If the time-to-failure of each component follows exponential distributions, each with a constant failure rate, ëi , i = 1, ... , n, the system reliability, assuming independence of component operation (failure of one does not impact failure of any other component), is given by
In a special case, where all components have the same failure rate, ë , the system reliability for parallel component is given by
For such specific situation, the mean-time-to-failure for the system with n identical components in parallel, and also assuming that each failed component is immediately replaced by an identical component, can be expressed as
Systems with Components in Series and in Parallel
Real life systems often consist of components that are mixed and consist of both series and parallel configuration. For such system, reliability calculation is primarily based on the previously discussed concepts, and assumption of components operating independently. Parallel systems are first collated to get a composite reliability, and then the overall components are considered as series to calculate system reliability. Systems can also consist of standby component, which operates as and when base component fails. Reader may refer to book by Amitava Mitra (2008) or Besterfield et al (2004 ) for further details on. K-out-of-N system (parallel system is 1 out of N system) is another possible system configuration.







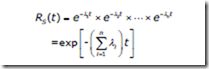





Comments
Post a Comment