What is robust design?

Module III Product Quality Improvement

Lecture – 4 What is robust design?

Dr. Genichi Taguchi, a mechanical engineer, who has won four times Deming Awards, introduced the loss function concept, which combines cost, target, and variation into one metric. He developed the concept of robustness in design, which means that noise variables (or nuisance variables or variables which are uneconomical to control) are taken into account to ensure proper functioning of the system functions. He emphasized on developing design in presence of noise rather than eliminating noise.

Loss Function

Taguchi defined quality as a loss imparted to society from the time a product is shipped to customer. Societal losses include failure to meet customer requirements, failure to meet ideal performance, and its harmful side effects.

Assuming the target [tau (ô )] is correct, losses are those caused by a product's critical performance characteristics, if it deviates from the target.The importance of concentrating on "hitting the target" is shown by Sony TV sells example. In spite of the fact that the design and specifications were identical, U.S. customers preferred the color density of shipped TV sets produced by Sony-Japan over those produced by Sony-USA. Investigation of this situation revealed that the frequency distributions were markedly different, as shown in Figure 3-13. Even though Sony-Japan had 0.3% outside the specifications, the distribution was normal and centered on the target with minimum variability as compared to Sony-USA. The distribution of the Sony- USA was uniform between the specifications with no values outside specifications. It was clear that customers perceived quality as meeting the target (Sony-Japan) rather than just meeting the specifications (USA). Ford Motor also had a similar experience with their transmissions.

Figure 3-13 Distribution of color density for Sony-USA and Sony-Japan

Out of specification is the common measure of quality loss in Goal post mentality [Figure 3-14 (a) ]. Although this concept may be appropriate for accounting, it is a poor concept for various other areas. It implies that all products that meet specifications are good, whereas those that do not are bad. From the customer's point of view, the product that barely meets the specification is as good (or bad) as the product that is barely just out-of-specification. Thus, it appears that wrong measuring system for quality loss is being used. The Taguchi’s loss function [Figure 3-14 (b)] corrects for the deficiency described above by combining cost, target, and variation into one single metric.

Figure 3-14(a): Discontinuos Loss Function (Goal Post Mentality)

Figure 3-14(b): Continuous Quadratic Loss function (Taguchi Method)

Figure 3-14(a) shows the loss function that describes the Sony-USA situation as per ‘Goal Post Mentality’ considering NTB (Nominal-the-Best)-type of quality charecteristic. Few performance characteristics considered as NTB are color density, voltage, bore dimensions, surface finish. In NTB, a target (nominal dimension) is specified with a upper and lower specification, say diameter of a engine cylinder liner bore. Thus, when the value for the performance characteristic, y, is within specifications the quality loss is $0, and when it is outside the specifications the loss is $A. The quadratic loss function as shown in Figure 3-14(b) describes the Taguchi method of definining loss function. In this situation, loss occurs as soon as the performance characteristic, y,

departs from the target, ô .

The quadratic loss function is described by the equation

Assuming, the specifications (NTB) is10 ± 3 for a particular quality characteristic and the average repair cost is $230, the loss coefficient is calculated as,

Average or Expected Loss

The loss described above assumes that the quality characteristic is static. In reality, one cannot always hit the target. It will vary due to presence of noise, and the loss function must reflect the variation of many pieces rather than just single piece. An equation can be derived by summing the individual loss values and dividing by their number to give

Where L = the average or expected loss, ó is the process variability of y charecteristic, y is the average dimension coming out of the process.

Because the population standard deviation, ó , is unknown, the sample standard deviation, s, is used as a substitute. This action will make the variability value somewhat larger. However, the average loss (Figure 3-15) is quite conservative in nature.

Figure 3-15 Average or Expected Loss

The loss can be lowered by reducing the variation, and adjusting the average, y, to bring it on target.

Lets compute the average loss for a process that produces shafts. The target value , say 6.40 mm and the loss coefficient is 9500. Eight samples give reading of 6.36, 6.40, 6.38, 6.39, 6.43, 6.39,6.46, and 6.42. Thus,

There are two other loss functions that are quite common, smaller-the-better and larger- the- better. In smaller-the-better type, the lesser the value is preferred for the characteristic of interest, say defect rate, expected cost, and engine oil consumption. Figure 3-16 illustrates the concept.

Figure 3-16 : (a) Smaller –the –Better and (b) Larger–the- Better-type of Loss Function

In case of larget-the-better, higher value is preferred for the characteristic of interest. Few examples of performance characteristics considered as larget-the-better are bond strength of adhesives, welding strength, tensile strength, expected profit.

Orthogonal Arrays

Taguchis method emphasized on highly fractionated factorial design matrix or Orthogonal arrays (OA) [http://en.wikipedia.org/wiki/Orthogonal_array] for experiment. This arrays are developed by Sir R. A. Fischer and with the help of Prof C R Rao (http://en.wikipedia.org/wiki/C._R._Rao) of Indian Statistical Institute, Kolkata. A L8 orthogonal array is shown below. An orthogonal array is a type of experiment where the columns for the independent variables are “orthogonal” or “independent” to one another.

Table 3-4 L8 Orthogonal Array

The 8 in the designation OA8 (Table 3-4) represents the number of experimental rows, which is also the number of treatment conditions (TC). Across the top of the orthogonal array is the maximum number of factors that can be assigned, which in this case is seven. The levels are designated by 1 and 2. If more levels occur in the array, then 3, 4, 5, and so forth, are used. Other schemes such as -1, 0, and +1 can be used. The orthogonal property of an OA is not compromised by changing the rows or the columns. Orthogonal arrays can also handle dummy factors and can be accordingly modified. With the help of OA the number of trial or experiments can be drastically reduced.

To determine the appropriate orthogonal array, we can use the following procedure,

Step-1 Define the number of factors and their levels.

Step-2 Consider any suspected interactions (if required).

Step-3 Determine the necessary degrees of freedom.

Step-4 Select an orthogonal array.

To understand the required degree of freedom, let us we consider four two-level (leveled as 1 and leveled as 2) factors, A, B, C, D, and two suspected interactions, BC and CD. Thus to determine the degrees of freedom or df, at least seven treatment conditions (experiments) are needed for the two-level,

df=4(2-1)+2(2-1)(2-1)+1=7

Selecting the Orthogonal Array

Once the degrees of freedom are known, factor levels are identified, and possible interaction to be studied, the next step is to select the orthogonal array (OA). The number of treatment conditions is equal to the number of rows in the OA and must be equal to or greater than the degrees of freedom. Table 3-5 shows the orthogonal arrays that are available, up to OA36. Thus, if the number of degrees of freedom is 13, then the next available OA is OA16. The second column of the table has the number of rows and is redundant with the designation in the first column. The third column gives the maximum number of factors that can be used, and the last four columns give the maximum number of columns available at each level.

Analysis of the table shows that there is a geometric progression for the two-level arrays of OA4, OA8, OAI6, OA32, ... , which is 22, 23, 24, 25, ... . For the three-level arrays of OA9, OA27, OA8I, ... , it is 32, 33, 34, ..... Orthogonal arrays can also be modified.

Table 3-5 Required Orthogonal Array

Interaction Table

Confounding is the inability to distinguish among the effects of one factor from another factor and/or interaction. In order to prevent confounding, one must know which columns to use for the factors in Taguchi method. This knowledge is provided by an interaction table, which is shown in Table 3-6.

Table 3-6 Interaction Table for OA8

Let's assume that factor A is assigned to column 1 and factor B to column 2. If there is an interaction between factors A and B, then column 3 is used for the interaction, AB. Another factor, say, C, would need to be assigned to column 4. If there is an interaction between factor A (column 1) and factor C (column 4), then interaction AC will occur in column 5. The columns that are reserved for interactions are used so that calculations can be made to determine whether there is a strong interaction. If there are no interactions, then all the columns can be used for factors. The actual experiment is conducted using the columns designated for the factors, and these columns are referred to as the design matrix. All the columns are referred to as the design space.

Linear Graphs

Taguchi developed a simpler method to work with interactions by using linear graphs.

Figure 3-17 Two linear Graphs for OA8

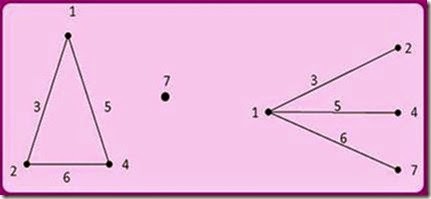
Two linear graph are shown in Figure 3-17 for OA8. They make it easier to assign factors and interactions to the various columns of an array. Factors are assigned to the points. If there is an interaction between two factors, then it is assigned to the line segment between the two points. For example, using the linear graph on the left in the figure, if factor B is assigned to column 2 and factor C is assigned to column 4, and then interaction BC is assigned to column 6. If there is no interaction, then column 6 can be used for a factor.

The linear graph on the right can be used when one factor has three two-level or higher order interactions. Three-level orthogonal arrays must use two columns for interactions, because one column is for the linear interaction and one column is for the quadratic interaction. The linear graphs-and, for that matter, the interaction tables-are not designed for three or more factor interactions, which are rare events. Linear graphs can also be modified. Use of the linear graphs requires some trial-and-error activity

Interactions

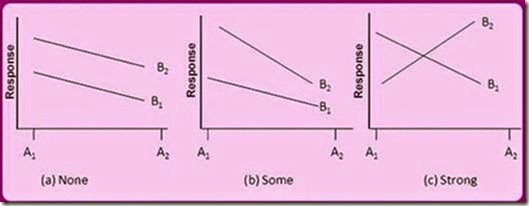
Interactions simply means relationship existing between different X-factors/X with noise variables considered for experiment. Figure 3-18 shows graphical relationship between any two factors. At (a) there is no interaction as the lines are parallel; at (b) there is little interaction existing between the factors; and at (c) there is a strong evidence of interaction. The graph is constructed by plotting the points A1B1 A2B2, A2B1 and A2B2.

Figure 3-18 Interaction between Two Factors

Signal-to-Noise (SIN) Ratio

The important contribution of Taguchi is proposing the signal-to-noise (S/N) ratio. It was developed as a proactive equivalent to the reactive loss function. When a person puts his/her foot on the brake pedal of a car, energy is transformed with the intent to slow the car, which is the signal. However, some of the energy is wasted by squeal, pad wear, and heat. Figure 3-19 emphasizes that energy is neither created nor destroyed.

Figure 3-19 Concept of Signal-to-Noise (S/N) Ratio

Signal factors (Y) are set by the designer or operator to obtain the intended value of the response variable. Noise factors (S2) are not controlled or are very expensive or difficult to control. Both the average, y, and the variance, s2, need to be controlled with it single figure of merit. In elementary form, S/N is y / s , which is the inverse of the coefficient of variation and a unit less value. Squaring and taking the log transformation gives

Adjusting for small sample sizes and changing from Bels to decibels for NTB type gives

There are many different S/N ratios. The equation for nominal-the-best was given above. It is used wherever there is a nominal or target value and a variation about that value, such as dimensions, voltage, weight, and so forth. The target (ô ) is finite but not zero. For robust (optimal) design, the S/N ratio should be maximized. The-nominal-the-best S/N value is a maximum when the average is near target and the variance is small. Taguchi's two-step optimization approach is to identify factors (X) which reduces variation of Y, and then bring the average (Y) on target by a different set of factor (X). The he S/N ratio for a process that has a temperature average of 21°C and a sample standard deviation of 2°C for four observations is given by

The adjustment for the small sample size has little effect on the answer. If it had not been used, the answer would have been 20.42 dB.

Smaller-the-Better

The S/Ns ratio for smaller-the-better is used for situations where the target value (ô ) is zero, such as computer response time, automotive emissions, or corrosion. The S/N equation used is

The negative sign ensures that the largest S/N value gives the optimum value for the response variable and, thus a robust design. Mean square deviation (MSD) is given to show the relationship with the loss function.

Larger-the-Better

The S/N ratio for larger-the-better type of characteristic is given by

Let us consider a battery life experiment. For the existing design, the lives of three AA batteries are calculated as 20, 22, and 21 hours. A different design produces batteries life of 17, 21, and 25 hours. To understand which is a better design (E or D) and by how much, we can use the S/N ratio calculation. As it is a larger-the-better (LTB) type of characteristic (Response), the calculation are

The different design is 7% better than existing design. More data will be required to confirm the result and so-called ‘Confirmatory trials’.

Although the metric signal-to-noise ratio have achieved good practical results, they are yet to be accepted universally as a valid statistical measure. The controversy is on measures and shape of loss function. However, Taguchi’s concept has resulted in a paradigm shift in the concept of product quality and can optimize without any empirical regression modeling concept.

It is also to be noted that inner (controllable factors) and outer array (for noise variable) design is recommended by Taguchi to understand the best setting for Robust Design, which many a times researchers omit for ease of experimentation. This practice may be avoided. Engineering

knowledge and idea of interaction is essential to get the best benefit out of OA design. For further details on Taguchi method, reader may refer the books written by P J Ross (1996), A Mitra (2008),Besterfield et at. (2004) and M Phatke (1995).